include/beecrypt/rsa.h File Reference
RSA algorithm. More...
#include "beecrypt/rsakp.h"
Include dependency graph for rsa.h:
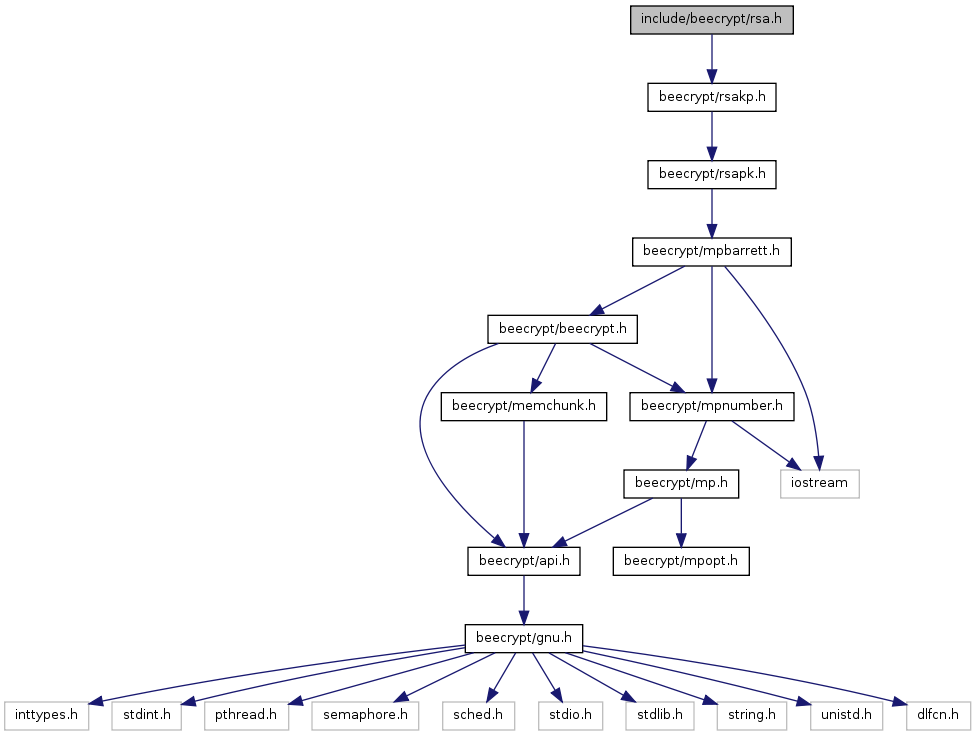
Go to the source code of this file.
Functions | |
| BEECRYPTAPI int | rsapub (const mpbarrett *n, const mpnumber *e, const mpnumber *m, mpnumber *c) |
| This function performs a raw RSA public key operation. | |
| BEECRYPTAPI int | rsapri (const mpbarrett *n, const mpnumber *d, const mpnumber *c, mpnumber *m) |
| This function performs a raw RSA private key operation. | |
| BEECRYPTAPI int | rsapricrt (const mpbarrett *n, const mpbarrett *p, const mpbarrett *q, const mpnumber *dp, const mpnumber *dq, const mpnumber *qi, const mpnumber *c, mpnumber *m) |
| This function performs a raw RSA private key operation, with application of the Chinese Remainder Theorem. | |
| BEECRYPTAPI int | rsavrfy (const mpbarrett *n, const mpnumber *e, const mpnumber *m, const mpnumber *c) |
| This function performs a raw RSA verification. | |
Detailed Description
RSA algorithm.
Function Documentation
This function performs a raw RSA private key operation.
This function can be used for decryption and signing.
It performs the operation:
- Parameters:
-
n The RSA modulus. d The RSA private exponent. c The ciphertext. m The message.
- Return values:
-
0 on success. -1 on failure.
| int rsapricrt | ( | const mpbarrett * | n, | |
| const mpbarrett * | p, | |||
| const mpbarrett * | q, | |||
| const mpnumber * | dp, | |||
| const mpnumber * | dq, | |||
| const mpnumber * | qi, | |||
| const mpnumber * | c, | |||
| mpnumber * | m | |||
| ) |
This function performs a raw RSA private key operation, with application of the Chinese Remainder Theorem.
It performs the operation:
- Parameters:
-
n The RSA modulus. p The first RSA prime factor. q The second RSA prime factor. dp dq qi c The ciphertext. m The message.
- Return values:
-
0 on success. -1 on failure.
This function performs a raw RSA public key operation.
This function can be used for encryption and verifying.
It performs the following operation:
- Parameters:
-
n The RSA modulus. e The RSA public exponent. m The message. c The ciphertext.
- Return values:
-
0 on success. -1 on failure.
This function performs a raw RSA verification.
It verifies if ciphertext c was encrypted from cleartext m with the private key matching the given public key (n, e).
- Parameters:
-
n The RSA modulus. e The RSA public exponent. m The cleartext message. c The ciphertext message.
- Return values:
-
1 on success. 0 on failure.

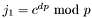
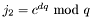
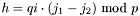

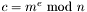
 1.5.8
1.5.8